斜率优化 dp 学习笔记

斜率优化，一个挺陌生的词汇，在 OI 中应用不是特别广泛，作为 dp 难题的形式出现在压轴位置上。

基本思路是通过对线性递推式的变化使之符合一个直线，并将最小/大化问题转化为截距最小问题（不着急，以后提及）。

如例题 「HNOI2008」玩具装箱。

在这道例题中，根据题面可以得到递推式：

这个式子是 的，递推下来是 。

为了优化降低复杂度，尝试拆开这个式子（设 ）：

提取出与 无关的东西放到左边，

也就是说，现在要最小化的仅为右边的这部分（ 是可以出 的因为与 无关）。

令左边为 ，，（拆开来是 。

全部带入原式，变成了：

也就是说，变成了最小化函数 过定点 且斜率为 的最小截距（y 轴交点最小化）。

首先，斜率仅关于 ，是定值；因此可以想象一个个平行的斜率过不同 的点时的不同位置（斜率和过点可以确定直线）。

想要找到最小值，那么直观的说，就是要找到在最下面的直线。

一系列 的点构成了一个下凸包。

如果选择的点不在下凸包上必定不是最优解。

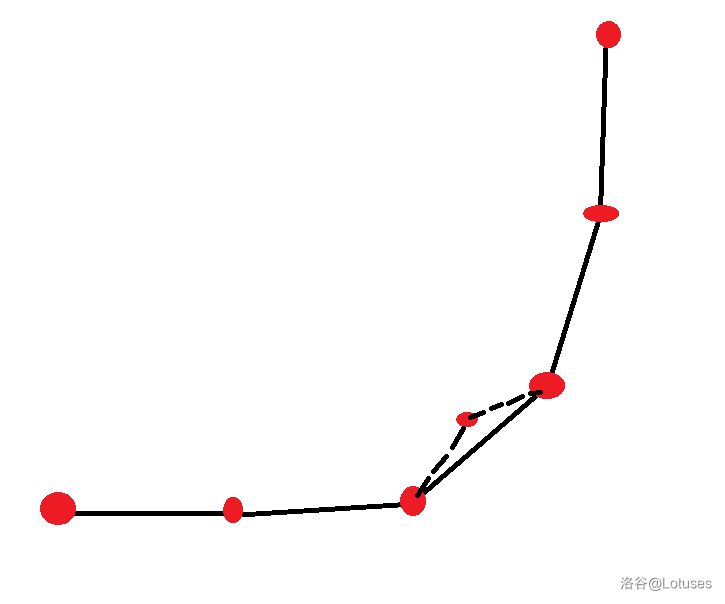
鄙人很菜，不会证明，只会臆测。理论上来说应该是正确的。

减少了很多点，现在只需要判断凸包上哪个点时最合适的。

由于是下凸包，斜率 严格非降，亲自移动一遍，应当某个点使左边的斜率比直线小，右边的斜率比直线大会在向上移动时刚好第一个碰到直线，是最优解。

由于斜率 在移动 时是递增的（ 不降）所以，夹在两个直线之间的点只会向后移动不会向前，那么这时候就想到了单调队列。

用单调队列维护相邻两个点的斜率 ，非降，因此总 维护这个最合适的点，均摊就是 。