Solution
关于某一条线段是否是安全的（以下不考虑端点），有两个结论。
- 不是平行于 的线段必定是安全的；
- 若这条线段中较低的点（即 坐标较小的点）下方没有其他边，那么这条线段必定是安全的。
第二条结论显而易见，可以直接从三角形正下方的点通过直线到达。
第一条结论，斜着的线段无论多斜，我都可以从线段两侧中任意选择一侧的点到达。
如图， 为原线段，延长 至 交 轴于 。在 左侧任意找一点 都可以通过直线到达 上的点 。
结合下两个结论，只有一种可能有不安全的线段。即：
一个三角形中，有一条线段平行于 ，并且还是三角形较高的边。
比如样例第三组数据，
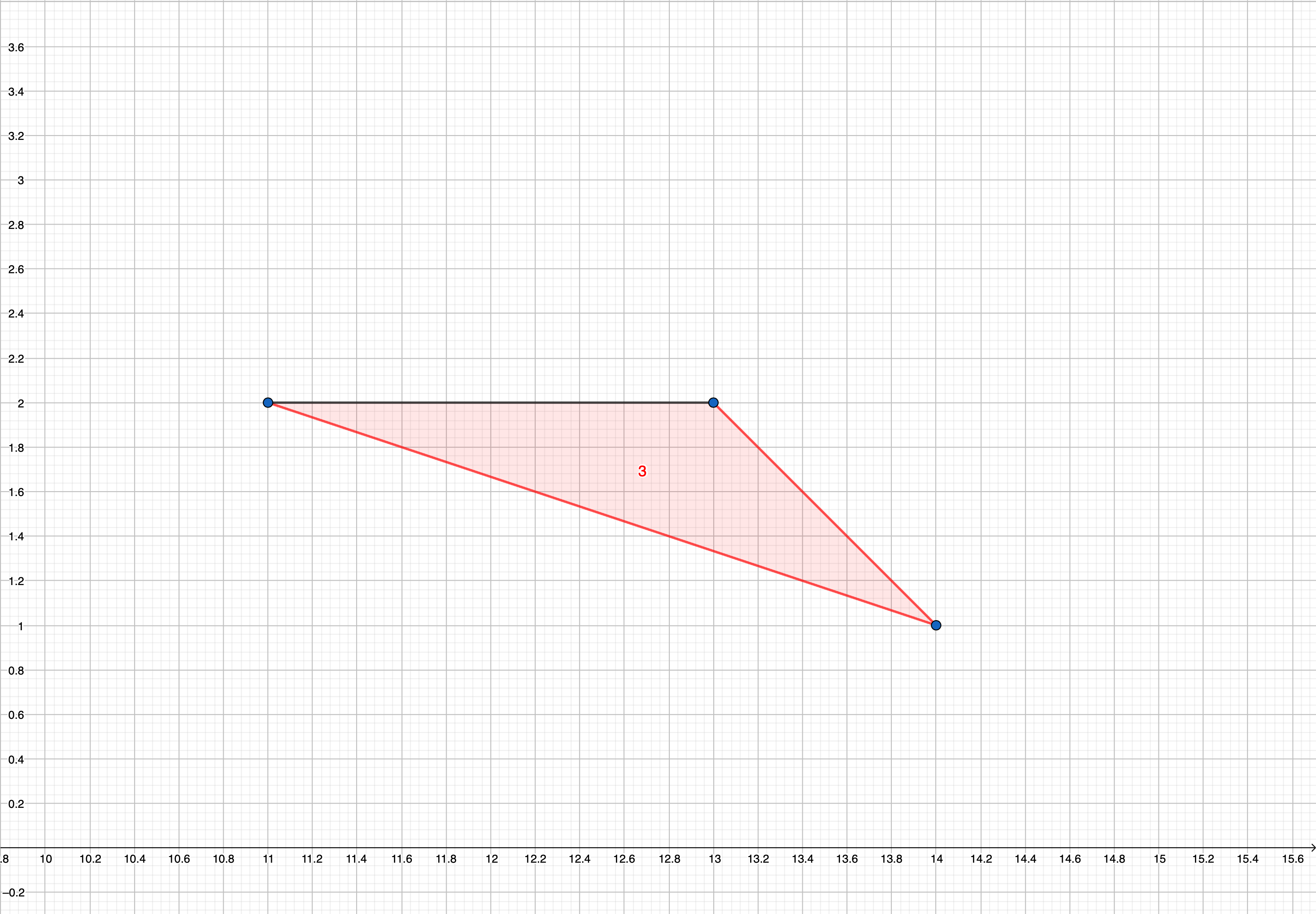
就是符合这些要求的三角形。
解法已经有了，如何更好的写更简单的代码呢？
用 struct 存端点，用 sort 简化代码。
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| #include<bits/stdc++.h>
using namespace std;
struct Point{
int x,y;
void read(){
cin>>x>>y;
}
bool operator < (Point b) const
{
if(y==b.y) return x>b.x;
return y>b.y;
}
}a[3];
int main()
{
int T;
cin>>T;
while(T--)
{
a[0].read();a[1].read();a[2].read();
sort(a,a+3);
if(a[0].y==a[1].y) cout<<abs(a[0].x-a[1].x);
else cout<<0;
puts("");
}
}
|
我有一个小疑问，题目中对浮点误差的处理有何意义？反正都是整数